Whale at MIT Museum
Sound | Research | Machines as a Medium
Works ⤑
Whale at MIT Museum
Whale is an acoustic and kinetic sculpture. It sings a 225-year-long song that is a weaving of songs of whales, neural network algorithms, and the twelfth century music of Hildegard von Bingen — who attributed much of her work to mystical forces beyond herself.
It is a meditation on end times, algorithms, visions, lives larger than our own, and the possibility that everything is alive.
No human will ever hear this long song. It’s made to fit in the lifespan of a bowhead whale.

Whale at Andy Cavatorta Studio with Marina Litvinskaya
fig. 1. The Destruction of Leviathan ― Gustave Doré (1865)

Around any current discussion of whales hovers
the growing possibility of their extinction. They
face their own very real end of days. But I want to
talk for a moment about the enormity of their lives.
Bowheads born today may live into the 23rd
century — living their own adventures together and
improvising their songs in a lifespan beyond our
imagining. They are social, like us, with long and
complex relationships. They are musically creative.
They are explorers.
Their lived adventure may last two and a half centuries. If collected, the songs sung and heard may exceed the length of a human life.
Whales are frequently associated with the mythical creature Leviathan (fig. 1) ― the enormous chaos monster that may lurk in the still of the deep of any sea. Whale and Leviathan are used interchangeably in myths from ancient times on up to Moby Dick. By extension, whales play a role in myths of the End Times.
“To the Leviathan God gave the seventh part of Earth filled with water, and He reserved it for the end of days when it shall be eaten by the righteous.”
― The Book of Enoch
“There is the music of Heaven in all things.”
― Hildegard von Bingen
The long song Whale sings grows from musical soil containing thousands of whale song recordings and the compositions of twelfth century polymath Hildegard von Bingen. Both are sources of nonhuman music with long perspectives on time.
Hildegard was born around 1098 and given to the
Benedictine monastery at Disibodenberg as an
oblate (spiritual servant). As a child, she was enclosed
(permanently walled-in) with another girl, Jutta. It was
common for enclosed persons to receive the Office of
the Dead upon entering, signifying their death to the
world. Both girls experienced ecstatic visions.
Hildegard eventually became a scholar and polymath.
Her documentation of her visions of the End Times (fig. 2)
were approved by Pope Eugenius III.
These visions also inspired her many musical
compositions and revealed to her that all matter is
alive.

fig. 2. Hildegard Of Bingen Receives A Vision ― Unknown Artist
If there are no mystical dimensions in the
Universe, if only the physical world exists,
then this does not negate our mysteries but instead
imbues matter with a numinous power. All of our
mysteries, including consciousness, must then be
emergent properties of matter.
The philosophical concept of panpsychism explores
the idea that all matter is conscious to some degree.
Can a machine have consciousness? The new
questions are the old questions.
This 16th century automaton in the form of a monk (fig. 3)
performs a complex perpetual ritual of devotion.
It marches ever forward in a trapezoidal pattern,
kissing a rosary, pounding its chest in penance, and
roughly mouthing “mea culpa” as its moving eyes
observe the moral world around it.
This machine was considered to be not just a
novelty but the personification of Saint Diego and
an extension of his spiritual mission beyond the
boundary of his earthly death.
fig. 3. Automaton in the Form of a Monk
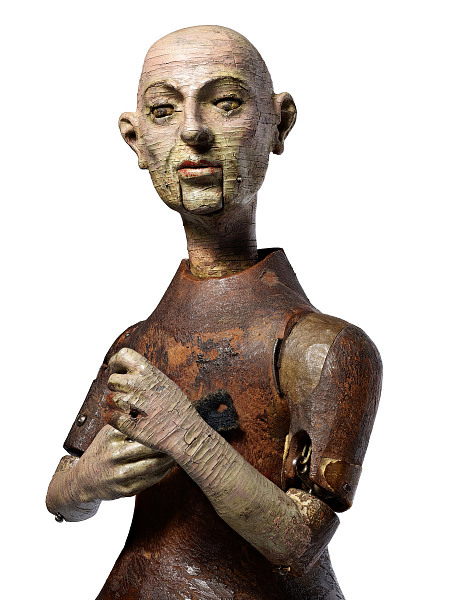

photos: National Museum of American History
Early sketch of Whale
Photo by Andrea De Santis

The collections of natural history museums are filled
with the spoils of the colonial conquest of both
human and animal kingdoms. The provenance of many
pieces is intertwined with the ending of a culture, a
people, or a species.
The skeletons of whales hanging in museums radiate
a sense of the wondrous, the tragic, and the eternal.
Especially the skeletons of cetaceans hunted to
extinction by humans seeking to convert their bodies
into money and exploitable energy — humanity’s
preferred forms of negative entropy.
Whale’s form is not separable from any of this history.
Even the language models and fungible processing
power used to dream its long song are inseparable from
the exploitable energy we are sacrificing to create our
AIs.
Can we invent a way of being that causes no suffering?
Blue whale skeleton in National History Museum in London

Concept for future project Against Eternity
Early sketch of Whale


Early sketch of Whale
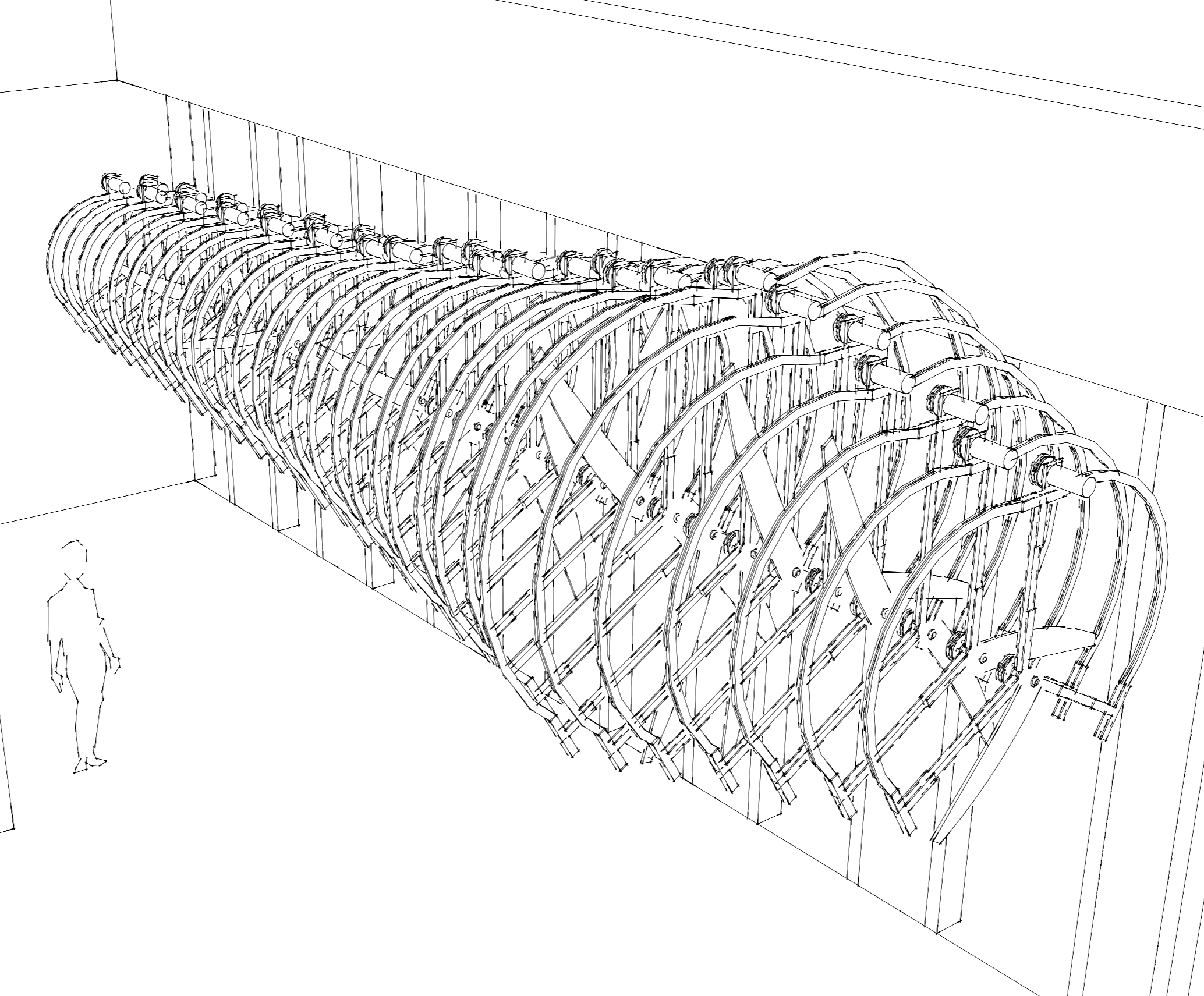
Whale’s 225 year-long song was composed by a recurrent
neural network trained on the compositions of Hildegard
von Bingen and recordings of the songs of Bowhead and
Humpback whales.
Hildegard's ~77 musical works were originally written as
neumes and lack notation for note length and musical key.
Modern reconstructions are based on scholarly research and
some likely guesses.
The whale songs come from audio data cataloged,
and shared by NOAA.
This music from whales and Hildegard was digitized and
encoded in the MIDI format — a lossy, reductive process
in both cases. These scores were then musically transposed to
use C as their root notes.
This corpus of scores was used to train a recurrent neural
network built with the Python library TensorFlow.
The resulting musical score is Whale's long song (fig. 4).
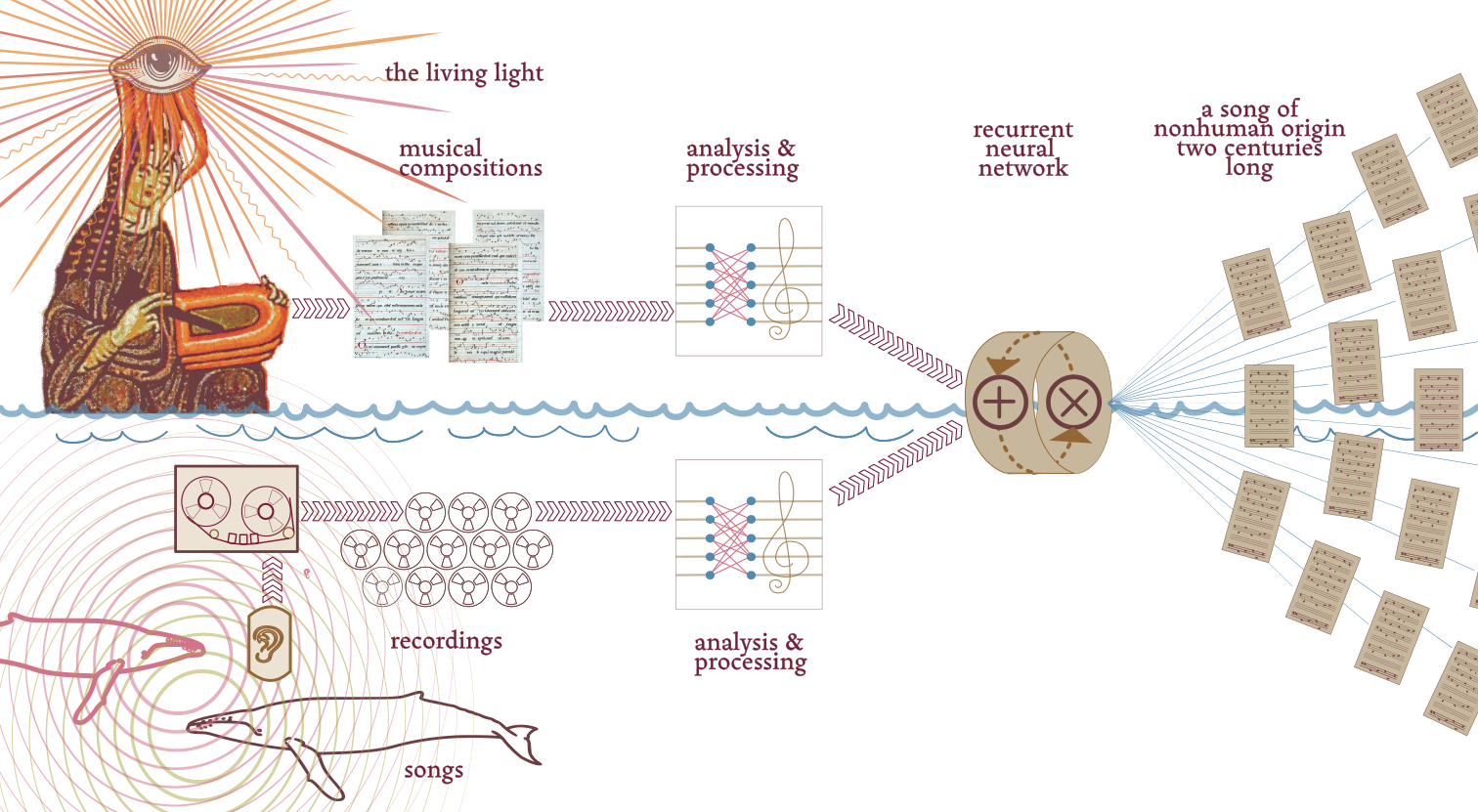
fig. 4.
When two or more waves overlap in the same space, the
resulting amplitude at any time is the sum of the wave
amplitudes at that time (fig. 5).
Overlapping waves can result in amplitudes higher
than either wave. This is called constructive interference.
Overlapping waves can also result in lower amplitudes or
even zero amplitude if the waves cancel
each other out. This is called destructive interference.
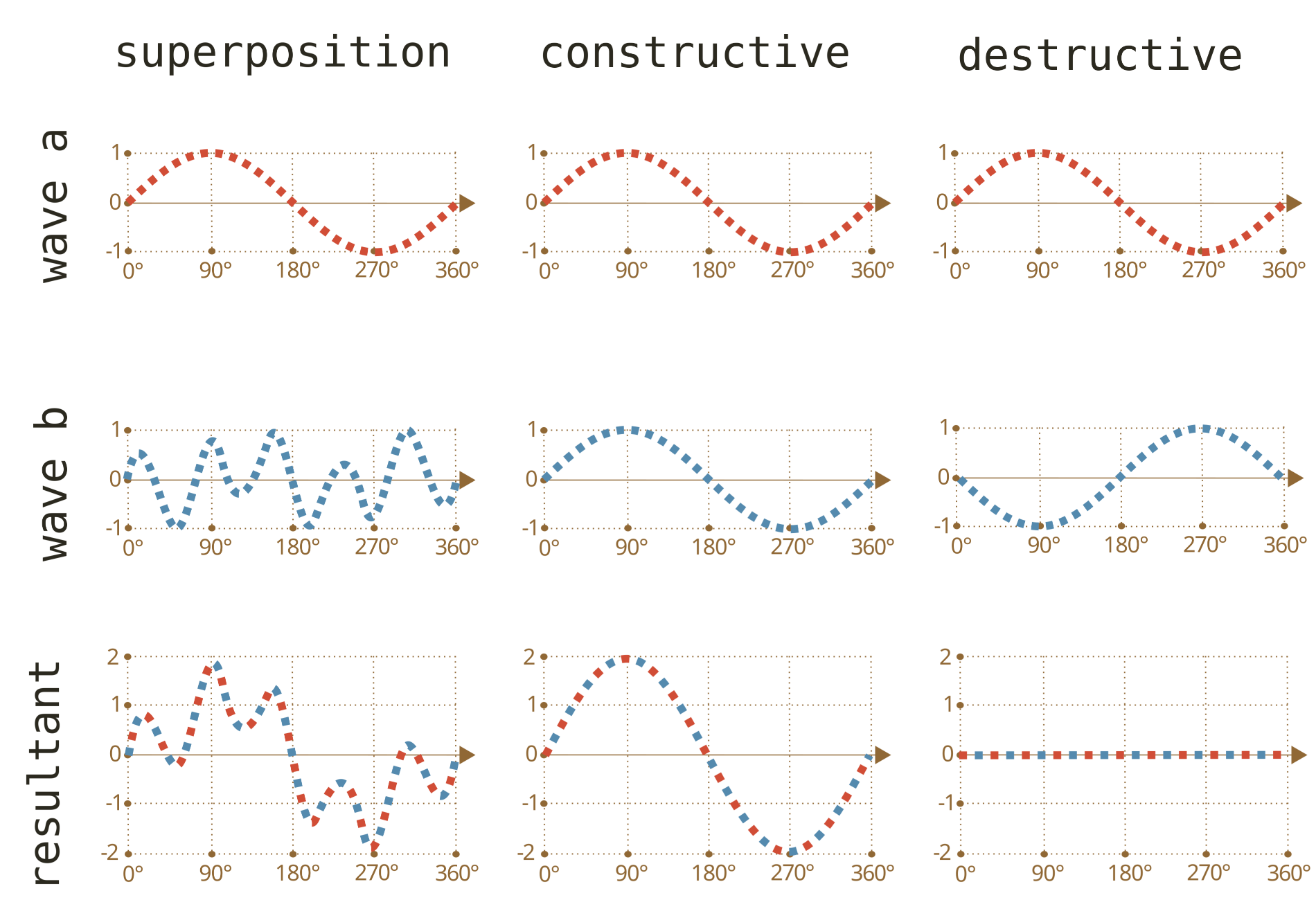
fig. 5.
Waves with similar frequencies traveling in opposite directions can combine to result in standing waves (fig. 6). A standing wave is a wave that oscillates in time but whose peak amplitude profile does not move in space. The points of small amplitude are called nodes. The points of high amplitude are antinodes.
The bottom row below shows a full cycle of standing
waves rising and falling.
All tuned acoustic instruments create stable tones
by creating standing waves in strings, membranes,
columns of air, or other mediums.
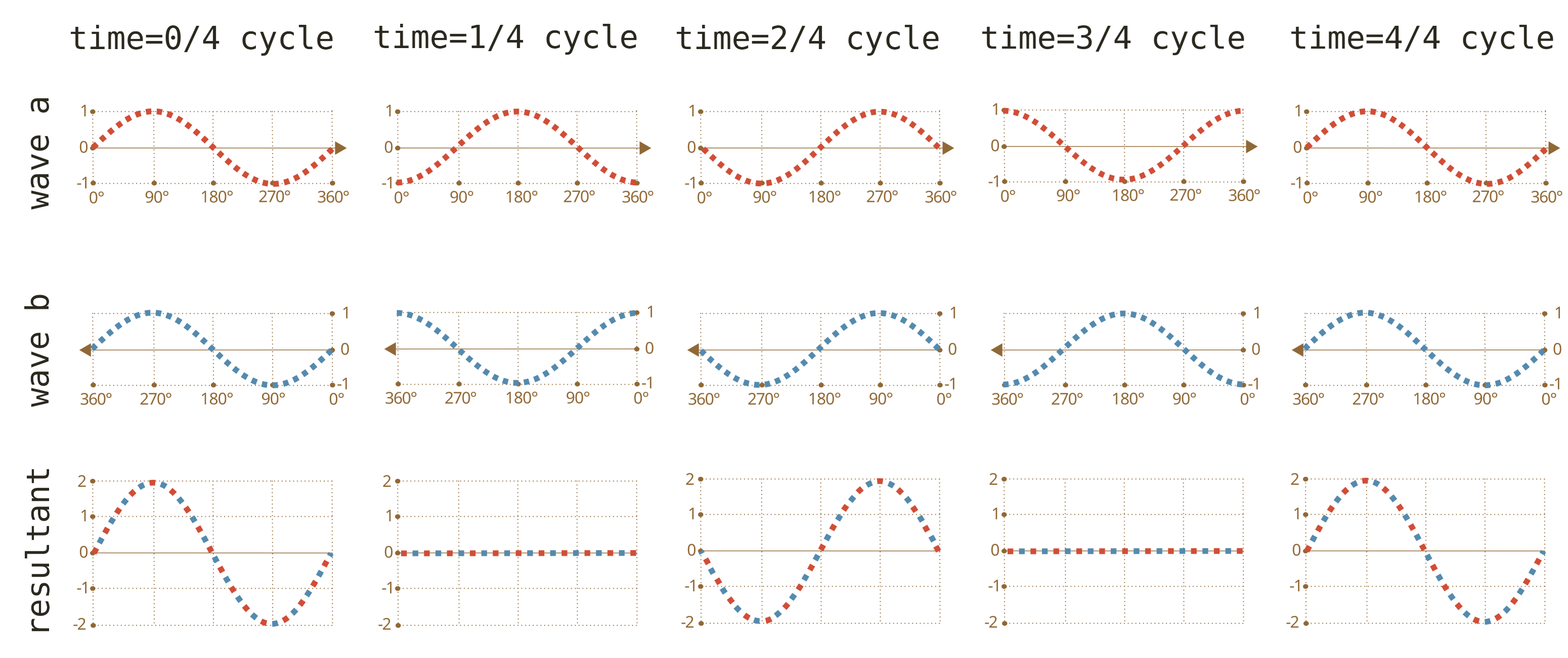
fig. 6.

fig. 7.
Air flowing through the tubes creates turbulent vortices as it passes over the corrugations. These create disorganized sound waves with a wide range of frequencies. (fig. 7)
The higher pressure wavefronts in the tube partially reflect back when they reach the lower pressure at the ends of the tubes (fig. 8). At certain energies, these create stable standing waves that organize the turbulent vortices around a dominant frequency. This process is called entrainment.
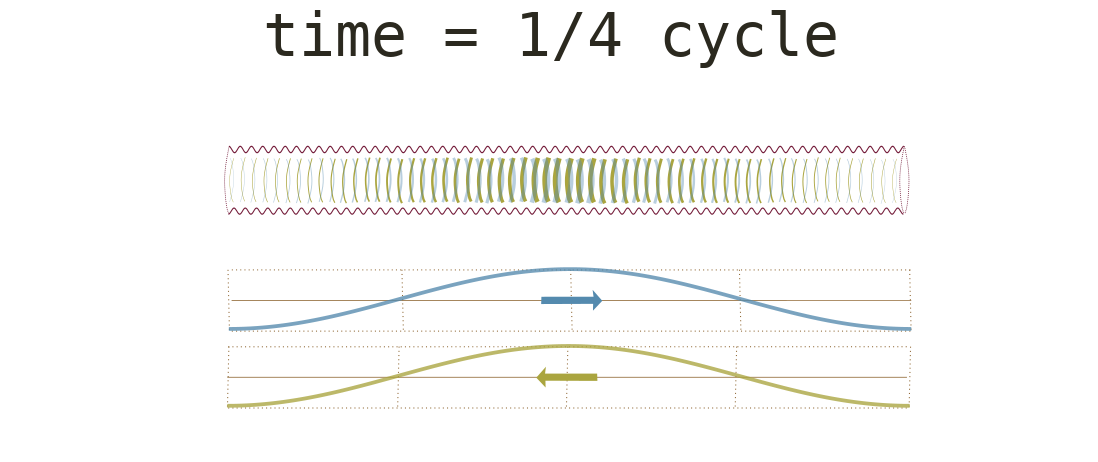
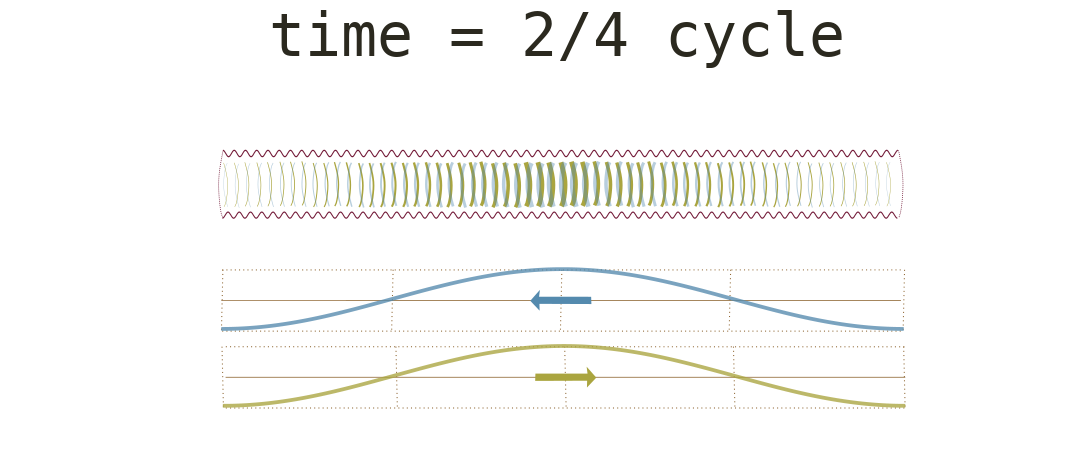
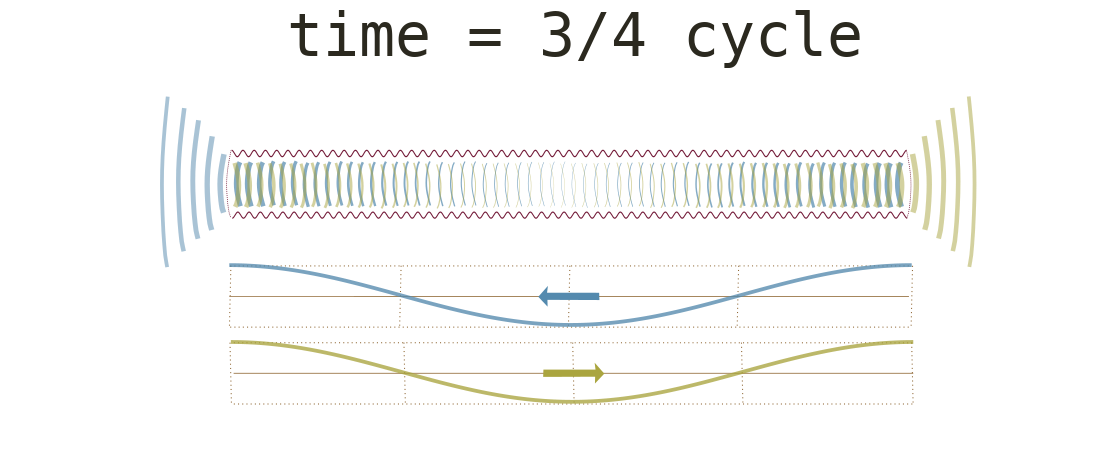
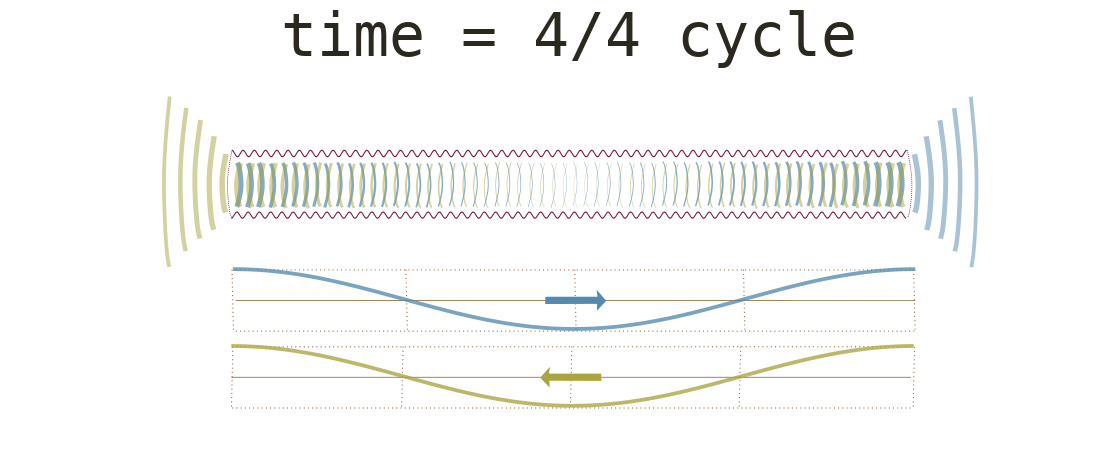
fig. 8.
All octaves are equidistant when viewed as musical pitch. The interval from A3 to A4 is the same size as the interval from A4 to A5.
But viewed as frequencies, each octave is double the frequency of the octave below it. Pitch and frequency have a logarithmic relationship (fig. 9).
The frequency difference between any two adjacent pitches is given by equation 1 below
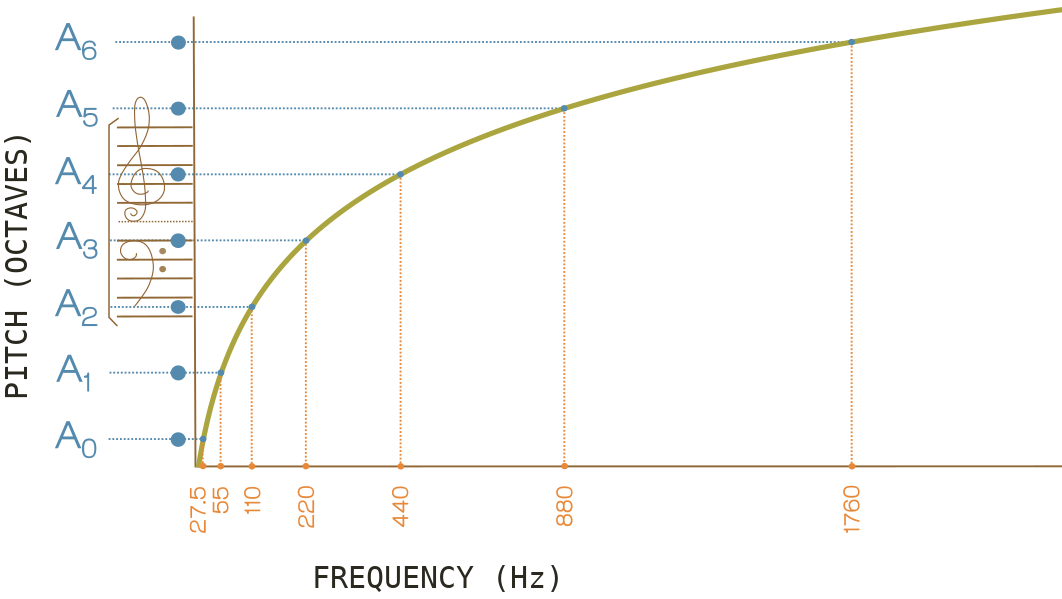
fig. 9.
equation 1: f(n) are the frequencies; n is the number of chromatic semitones between the pitches

fig. 10.
fig. 10 above illustrates a blue sound wave originating in a tube (left) and propagating two more wavelengths to the right. The Greek letter lambda (λ) is the standard physics symbol for wavelength.
Wavelength measures the physical length of a wave. Frequency measures the temporal length of a wave. The faster a wave of a certain length propagates through its medium, the shorter its frequency (equation 2)
equation 2: λ is the wavelength; v is the speed of sound in air; f is the frequency
As air flows faster through the tube, the energy in the vortices increases. This can cause the standing waves to jump to a higher harmonic mode with more nodes (fig. 11). This pattern of increasing nodes and pitches is called the Harmonic Series.
The next mode is called the second harmonic or h2 mode. This corresponds to a wavelength equal to the length of the tube. It produces a pitch one octave above the fundamental.
The lowest harmonic mode is called the fundamental or h1 mode. In open-ended tubes, this corresponds to a wavelength twice as long as the tube.
The third harmonic (h3) corresponds to a wavelength that is one third as long as the fundamental, making it two thirds the length of the tube. It produces a pitch that is one octave plus one perfect fifth above the fundamental.
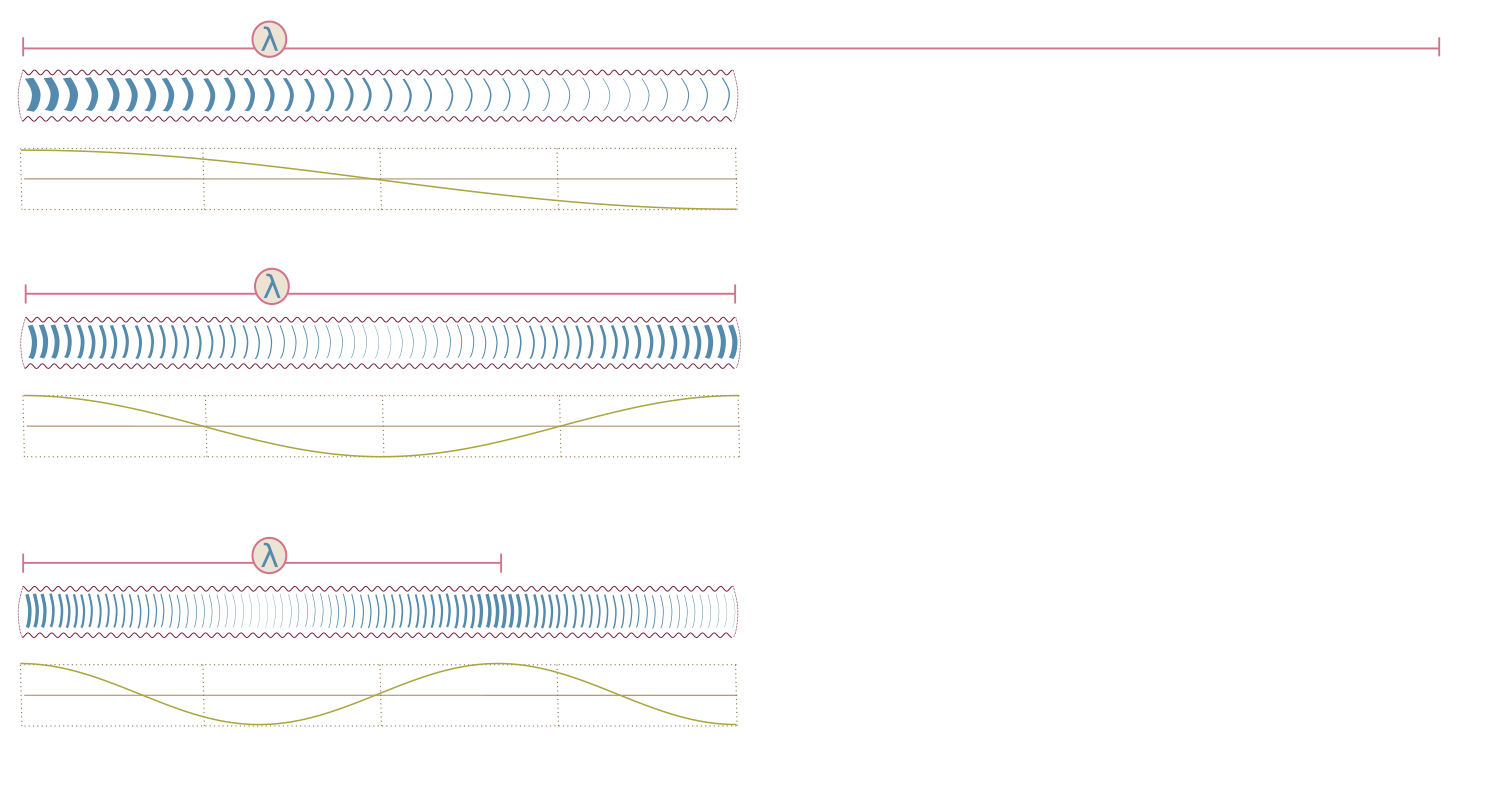
fig. 11.
When we substitute f in equation 2 with its value from equation 1, we get a formula for calculating the length of a tube to produce a specific musical pitch. This is equation 3 below.
The table below (fig. 12) shows the lengths of all of Whale's tubes.
It also shows the pitches of the second and third harmonics for each tube length.
equation 3: λ is the wavelength; n is the number of chromatic semitones between the pitches
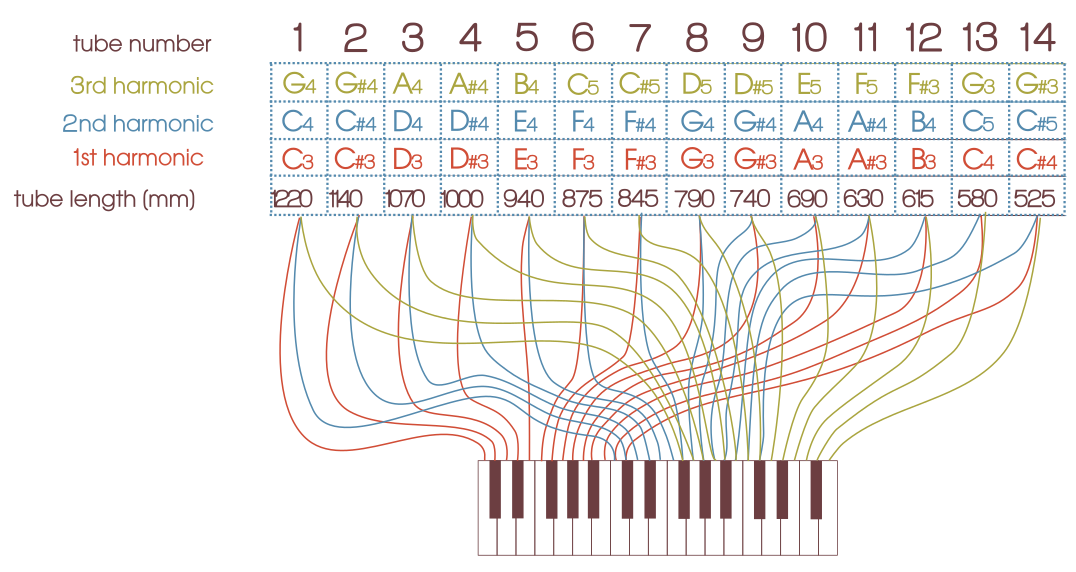
fig. 12.







